资料分析 2
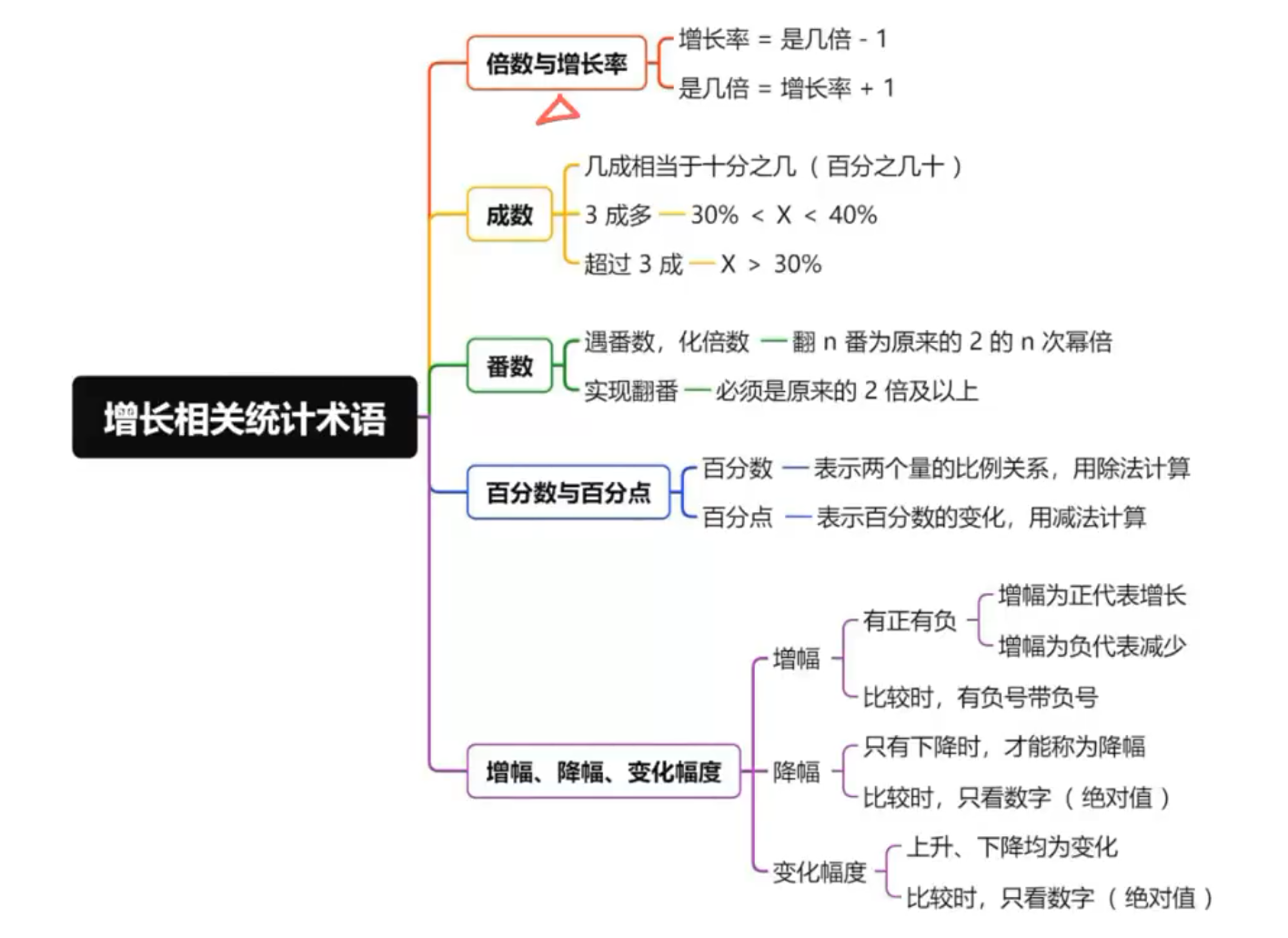
倍数与增长率公式
1. 倍数计算
A 是 B 的几倍:
示例:
- 2024 年工资
元,2023 年工资 元。 - 计算:
即 2024 年工资是 2023 年的 1.2 倍。
2. 增长率计算
核心公式
A 比 B 的增长率:
示例:
2024 年工资
计算:
即 2024 年工资比 2023 年 增长 20%。
如果给现期和增长量,比较增长率。
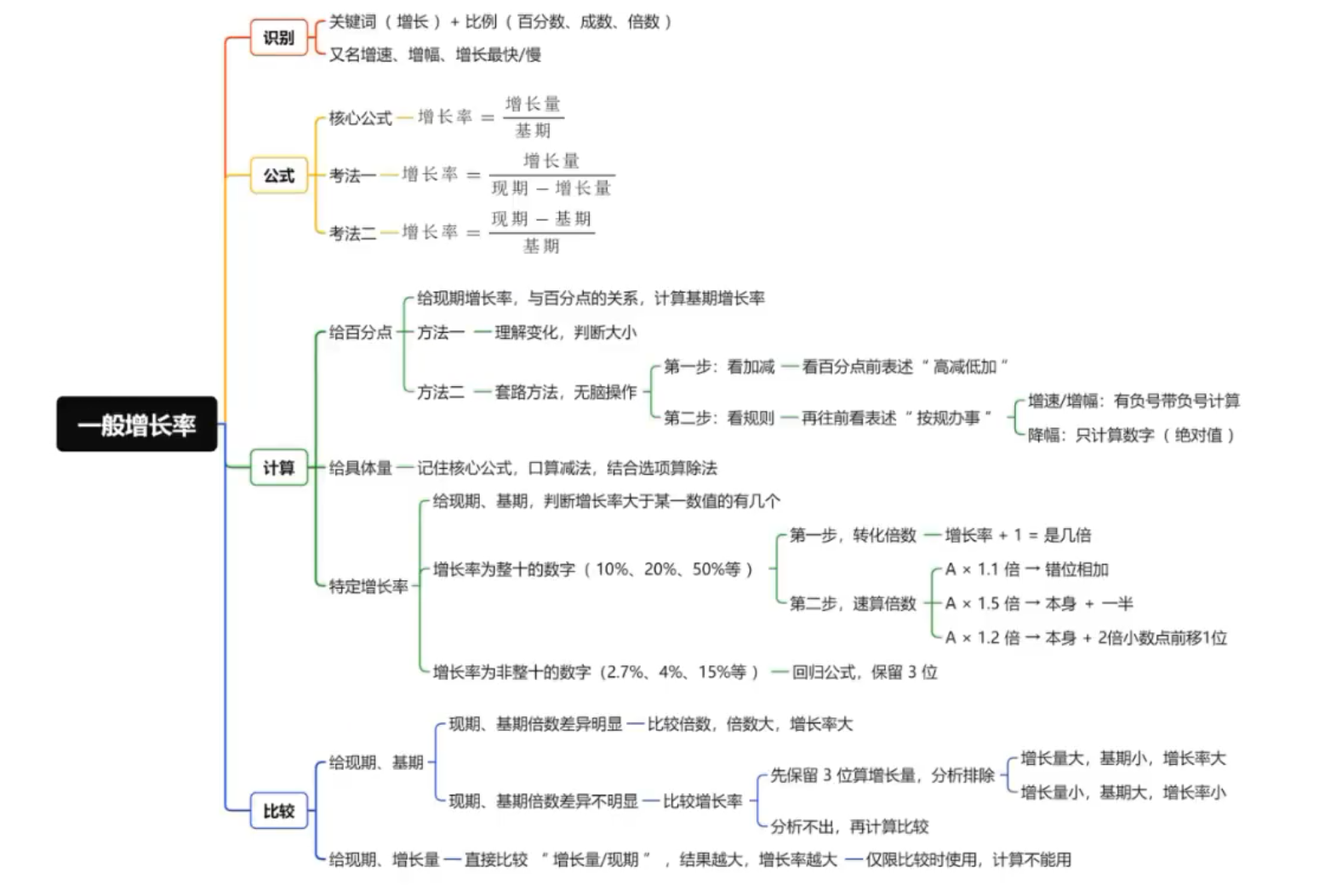
增长率计算公式
方法
直接比较:
结果越大,增长率越大。
3. 倍数与增长率的关系
- 增长率 = 倍数 - 1
- 倍数 = 增长率 + 1
成数
几成相当于十分之几
番数
遇 番数化倍数,翻
特定增长率: 给现期、基期, 判断增长率大于某一数值的有几个。


给现期、基期,比较增长率
| 情况 | 条件 | 比较方式 |
|---|---|---|
| 情况一 | 现期、基期倍数差异明显 | 比较倍数 |
| 情况二 | 现期、基期倍数差异不明显 | 比较增长率 |
 |
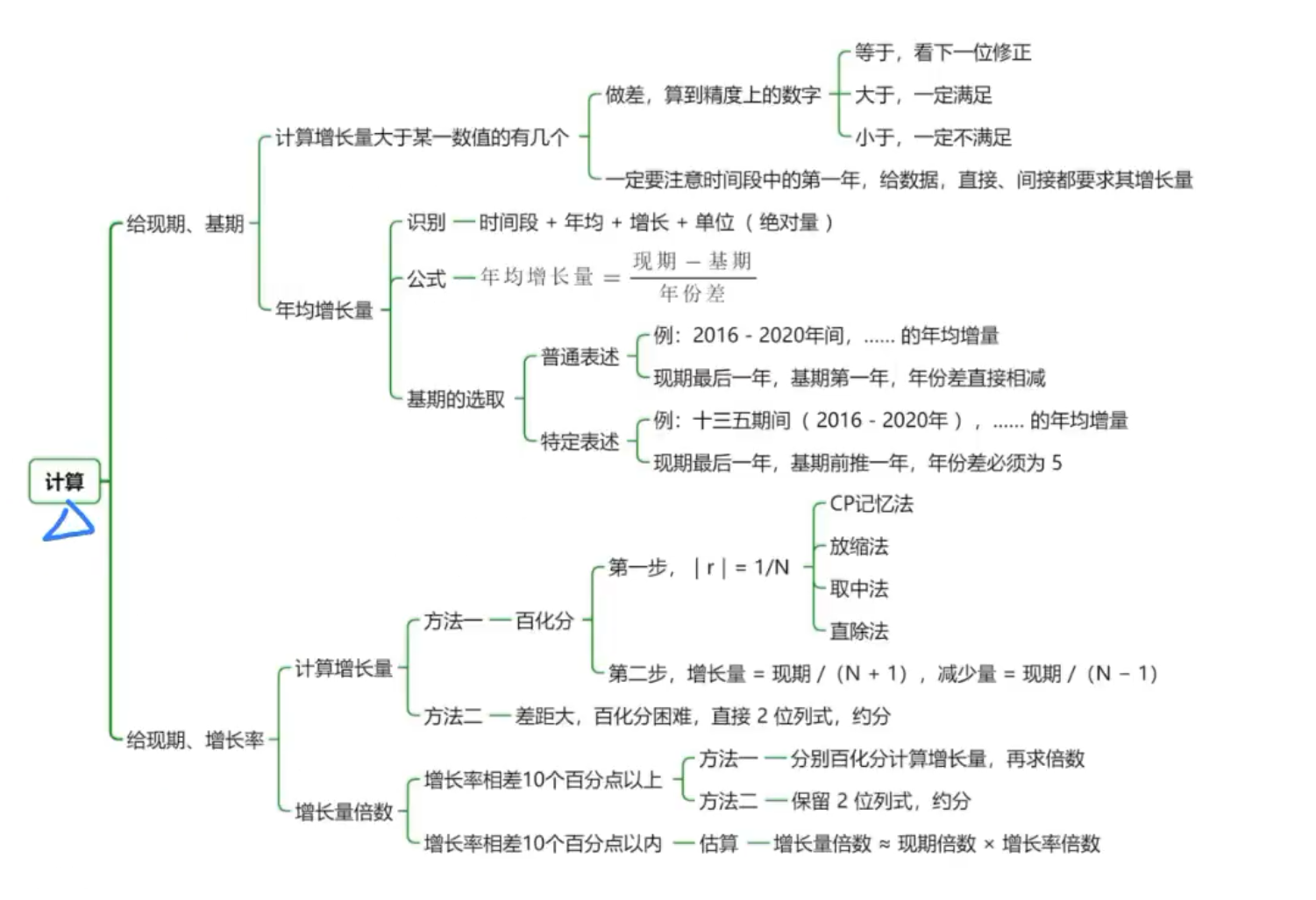
增长量的公式
给基期,现期,计算年均增长量
1. 识别特征
- 关键词:时间段 + 年均 + 增长 + 单位(绝对量)
- 典型问题:某时间段内,年均增长量是多少?
2. 计算公式
- 现期:所给时间段的最终值
- 基期:所给时间段的起始值
- 年数:时间段的总年数$$(\text{现期年份} - \text{基期年份})$$
3. 适用场景
- 计算 年均增长量,用于描述 增长的绝对值,例如 GDP、产值等。
- 适用于 总量分析,不涉及百分比。
4. 例题
- 2017 - 2021 年间,广东农林牧渔业总产值年均增加 多少亿元?
- “十三五” 期间,我国集成电路出口额的年均增量是多少?
已知现期,增长率,求增长量。
计算增长量方法
1. 适用场景
- 已知 现期值 和 增长率,求 增长量 或 减少量。
2. 计算方法
第一步:确定增长率比值
第二步:计算增长量 / 减少量
- 增长量计算
- 减少量计算
3. 适用场景
- 同比增长:按照增长率计算新增量。
- 同比减少:按照减少率计算减少量。
常用百化分
给现期,增长率,计算增长量的倍数。
计算增长量的倍数方法
方法
-
增长率相差 10 个百分点以上:
- 分别百分化 计算增长量,再求倍数。
-
增长率相差 10 个百分点以内:
- 近似计算:
- 近似计算:
示例对比
| 情况 | 2024 年A工资 | 增长率 | 2024 年B工资 | 增长率 | 计算增长量倍数 |
|---|---|---|---|---|---|
| 例 1 | 200 元 | 50% | 100 元 | 5% | 需分别计算增长量,再求倍数 |
| 例 2 | 200 元 | 10% | 100 元 | 5% | 近似计算 (上面公式) |
| 📌 增长率差距决定计算方式: |
- 差距大 → 直接计算增长量
- 差距小 → 近似计算
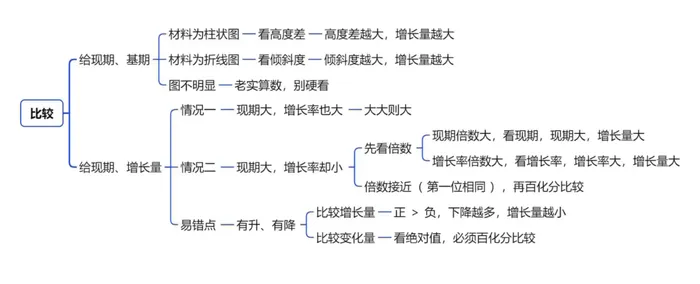
给现期,基期,比较增长量。
材料为折线图、柱状图。
图不明显,或者材料仅为数字。
情况一 现期大,增长率也大。
情况二 现期大,增长率小。
优先比较倍数:如果倍数接近(首位相同),再进行百分化分比较。